雙語核對:雙語核對師依照原文檢查譯文是否正確,並修正錯誤
It is observedfrom frequent experimentation that drawing pulling 1identicalbars from steeland rubber by the same axial force,and consequentlythe sameaxial stress, results of stress indifferent elongations from the two bars. In mechanics, the differences difference inthe materials 2of the two bars is represented by the relationship betweenthe components of stress and the strain. TheBywriting each ofthese likeasa matrix of column matrix,i.e.,3
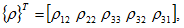 (1)
(1)
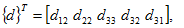 (2)
(2)
we have
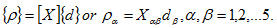 (3)
(3)
where X is a 5 x 5 matrix that characterizes thematerial of the body, and is generallycalled the matrix of elasticityand itscomponents are called elasticity’s elasticities 4or elastic constantsof elasticity 5for the material of the body.Note that shear strains have been multiplied by 2 in eqn. (2); the definitions (1) and(2) make ensure6 that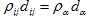 .
. Theequation (3), in other words the relation between the stresses and strains, areiscalled the relationconstitutive relation for the material of the body.It is assumed in Eq. (3) that the body is stress free in the reference configuration of reference from which the strain d is measured.
編修:英文母語編修師改善文章整體的流暢度與呈現方式
It is observed from fFrequent1experimentation has shown that drawing pulling 2the identical barsof from steel and rubber having the same initial lengths by the sameaxial force, and consequently thus thesame axial stress, results ofstress in different elongations from of these two bars. In mechanics, the differences difference in the materials 3of the two bars is represented by the relationship betweenthe components of stress and the strain.TheBywritingexpressing 4each of these likeasa matrix of column matrix5,i.e.,6
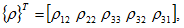 (1)
(1)
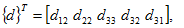 (2)
(2)
we haveobtain
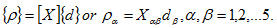 (3)
(3)
whereHere,X is a 57 x× 5 matrix that characterizes thematerial of the body,and is generally. It is generally calledknown asthe matrix of elasticity andmatrix;8 itscomponents are called elasticity’s elasticities 9or elastic constants10of elasticity forthe material of the body. Note thatThe shear strains have been multiplied by 2 in eqn.Eq. (2); the definitions (1)and (2) makeensure11 that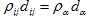 .
. Thestress-strainequation (3), in other words the relation shown inbetween the stresses and strains, are Eq. (3) is called known as therelation constitutiverelationfor the material of the body. 12It is assumed in Eq. (3) that thebody is stress-13free in the reference configuration of reference fromwhich the strain d is measured.